Mastery & Spiralling
The two most common approaches for planning and teaching math are (1) mastery and (2) spiralling. Through the mastery approach, students learn math in an incremental manner with one skill building on another. Furthermore, students have to understand the first competence with high mastery before moving onto the next competence. The unit (e.g. fractions) is taught in consecutive lessons or however many days/weeks it takes to master. The teacher moves through the year chapter by chapter. Conversely, spiralling a unit (e.g. perimeter and area) that can be done in lessons across the year. Therefore, the content is revised in intervals with more depth being added each time, in addition to providing the teacher an opportunity to reteach, if necessary. The Granite State Home Educators blog (2017) explains it the best, "Mastery approaches seek to build a complete set of knowledge, and then build upon those foundation blocks. Spiral approaches teach a concept to a certain level and then move on in order to offer exposure to topics before building further on the initial topics."
I first read about spiralling on the blog, One Stop Teacher Shop. Spiralling is a teaching strategy developed and researched by Jerome Bruner. Everyday Mathematics defines spiralling as "learning [that] is spread out over time rather than being concentrated in shorter periods." In a unit, spiralling curriculum is repeated and revisited instead of being taught in a particular block. Imagine teaching fractions in the first week of the unit and then coming back to fractions in the third week. The third week lesson can be a revision of the first week lessons on fractions, in addition to having new material that requires the knowledge from the previous lessons. And then we can teach fractions in another unit for students to revisit the concept. This way, students tend to remember the topic a lot better. To learn more about spiralling the following are some useful links: Teaching in Room 6, The Homeschool Post, and One Stop Teacher Shop.
There is, however, much debate around the method that works better for students. According to Maths Australia, "While both approaches to maths mastery strive for similar outcomes, Western education systems can attest to the inherent shortcomings in the spiral approach. In the 1990s, when the U.S. began participating in international testing for maths, they discovered that U.S. students performed significantly lower than other students. Much of this is attributed to the spiral approach to teaching. Countries that preferred a mastery approach such as Japan and Finland produced top-performing students! Subsequently, Western educational programs, educators, and textbook publishers begin to support the mastery approach to teaching math." Conversely, the mastery approach is critiqued for being too focused on individual concepts without looking at the broader picture, providing little space to review material, and few opportunities to focus in depth on topics, which the spiralling method claims to do.
Typically, when teachers reach out about instructional and pedagogical advice, I am often able to use my own experiences as a teacher to provide insight into what might and might not work. Here, I am less confident. I have tried both the mastery and spiralling approach, finding pros and cons in both of the approaches.
I first read about spiralling on the blog, One Stop Teacher Shop. Spiralling is a teaching strategy developed and researched by Jerome Bruner. Everyday Mathematics defines spiralling as "learning [that] is spread out over time rather than being concentrated in shorter periods." In a unit, spiralling curriculum is repeated and revisited instead of being taught in a particular block. Imagine teaching fractions in the first week of the unit and then coming back to fractions in the third week. The third week lesson can be a revision of the first week lessons on fractions, in addition to having new material that requires the knowledge from the previous lessons. And then we can teach fractions in another unit for students to revisit the concept. This way, students tend to remember the topic a lot better. To learn more about spiralling the following are some useful links: Teaching in Room 6, The Homeschool Post, and One Stop Teacher Shop.
There is, however, much debate around the method that works better for students. According to Maths Australia, "While both approaches to maths mastery strive for similar outcomes, Western education systems can attest to the inherent shortcomings in the spiral approach. In the 1990s, when the U.S. began participating in international testing for maths, they discovered that U.S. students performed significantly lower than other students. Much of this is attributed to the spiral approach to teaching. Countries that preferred a mastery approach such as Japan and Finland produced top-performing students! Subsequently, Western educational programs, educators, and textbook publishers begin to support the mastery approach to teaching math." Conversely, the mastery approach is critiqued for being too focused on individual concepts without looking at the broader picture, providing little space to review material, and few opportunities to focus in depth on topics, which the spiralling method claims to do.
Typically, when teachers reach out about instructional and pedagogical advice, I am often able to use my own experiences as a teacher to provide insight into what might and might not work. Here, I am less confident. I have tried both the mastery and spiralling approach, finding pros and cons in both of the approaches.
Planning a Math Unit
Whether you use the mastery or spiralling approach to planning a unit, a math unit plan is a helpful plan to span out the different expectations or objectives for the specific grade level. Every teacher has a different way of approaching unit planning. I prefer to plan all units for four (4) weeks, specifically using the thematic units for any and all language arts. As a result, I also plan math units for four weeks.
Step 1: Curriculum and Objective Planning
The first step to planning a math unit is to look at the curriculum documents and then selecting the expectations/objectives from there. Let us take, for example, the Ontario Math Curriculum for Grade 3. The document highlights five major strands: number sense and numeration, measurement, geometry and spatial sense, patterning and algebra, and data management and probability (Ontario Ministry of Education, 2005, p. 53). Each of these strands is then further detailed into overall expectations and specific expectations. The Ontario curriculum usually outlines about 10-15 overall expectations, which are the major expectations of the broader five strands. These overall expectations are then further broken down into even more detailed, specific expectations. These specific expectations or objectives are the ones we teach in our daily lesson.
Using the Measurement strand for Grade 3 (Ontario Ministry of Education, 2005, p. 57), it can be noticed that there are two overall expectations: (1) estimate, measure, and record length, perimeter, area, mass, capacity, time, and temperature, using standard units and (2) compare, describe, and order objects, using attributes measured in standard units. Each of these overall expectations includes several specific expectations, which are essentially telling us what our students will be able to do. One specific expectation, for example, outlines that students will be able to "draw items using a ruler, given specific lengths in centimetres" (Ontario Ministry of Education, 2005, p. 57). Again, it is this specific expectation that is used to draft a daily lesson plan.
Considering the strands and overall expectations, what specific expectations (or objectives) do we focus on for the unit? I personally focus on one strand for two (2) weeks in the unit plan and then another strand for the other two (2) weeks, using the spiralled approach to math. Therefore, students learn about measurement and then move to number sense and numeration, as an example. I would then come back to the measurement strand in another unit plan in the year, going into more depth. Then, how do we select the expectations for those two (2) weeks. Here, I suggest looking at the curriculum document and starting with the preliminary requisites. For example, it does not make sense for students to start by drawing a specific measurement with a ruler, if they do not know how to measure using a ruler.
Step 2: Calendaring Unit by Unit
The second step is to look at the calendar and plan out the math block, which includes the expectations (or objectives) for the curriculum, as mentioned above, and the other components of the math block (i.e. activities and drills, number talk, and so on). Calendaring the unit plan really requires an understanding of the students, and, in many ways, some guesswork. However, the guesswork should be based on reasoning. Here, what I mean is essentially thinking about how to disperse the specific expectations across the week and then the unit. Some specific expectations may only require one single math lesson while others will take 2-3 lessons to learn.
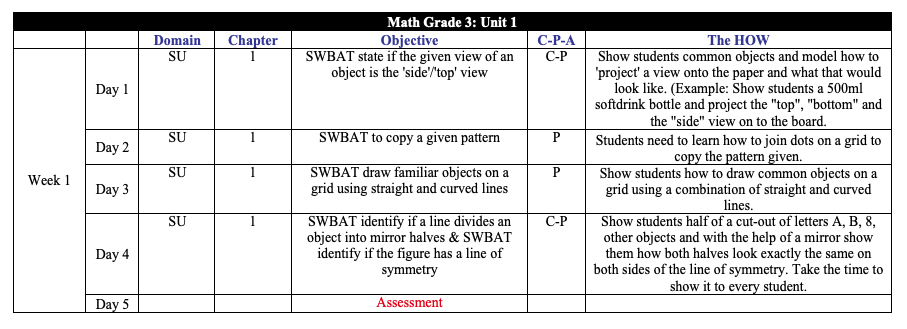
The unit is essentially several weeks. For me, they tend to be three to four weeks long. In order to calendar the objectives, I use a template like the one below and here is a sample math unit plan (without specific dates). The example below is one week of the unit and all the weekly plans together make the unit plan for those weeks. This week-by-week breakdown serves as a checklist of all the objectives that I will try to cover in the unit.
Step 1: Curriculum and Objective Planning
The first step to planning a math unit is to look at the curriculum documents and then selecting the expectations/objectives from there. Let us take, for example, the Ontario Math Curriculum for Grade 3. The document highlights five major strands: number sense and numeration, measurement, geometry and spatial sense, patterning and algebra, and data management and probability (Ontario Ministry of Education, 2005, p. 53). Each of these strands is then further detailed into overall expectations and specific expectations. The Ontario curriculum usually outlines about 10-15 overall expectations, which are the major expectations of the broader five strands. These overall expectations are then further broken down into even more detailed, specific expectations. These specific expectations or objectives are the ones we teach in our daily lesson.
Using the Measurement strand for Grade 3 (Ontario Ministry of Education, 2005, p. 57), it can be noticed that there are two overall expectations: (1) estimate, measure, and record length, perimeter, area, mass, capacity, time, and temperature, using standard units and (2) compare, describe, and order objects, using attributes measured in standard units. Each of these overall expectations includes several specific expectations, which are essentially telling us what our students will be able to do. One specific expectation, for example, outlines that students will be able to "draw items using a ruler, given specific lengths in centimetres" (Ontario Ministry of Education, 2005, p. 57). Again, it is this specific expectation that is used to draft a daily lesson plan.
Considering the strands and overall expectations, what specific expectations (or objectives) do we focus on for the unit? I personally focus on one strand for two (2) weeks in the unit plan and then another strand for the other two (2) weeks, using the spiralled approach to math. Therefore, students learn about measurement and then move to number sense and numeration, as an example. I would then come back to the measurement strand in another unit plan in the year, going into more depth. Then, how do we select the expectations for those two (2) weeks. Here, I suggest looking at the curriculum document and starting with the preliminary requisites. For example, it does not make sense for students to start by drawing a specific measurement with a ruler, if they do not know how to measure using a ruler.
Step 2: Calendaring Unit by Unit
The second step is to look at the calendar and plan out the math block, which includes the expectations (or objectives) for the curriculum, as mentioned above, and the other components of the math block (i.e. activities and drills, number talk, and so on). Calendaring the unit plan really requires an understanding of the students, and, in many ways, some guesswork. However, the guesswork should be based on reasoning. Here, what I mean is essentially thinking about how to disperse the specific expectations across the week and then the unit. Some specific expectations may only require one single math lesson while others will take 2-3 lessons to learn.
The unit is essentially several weeks. For me, they tend to be three to four weeks long. In order to calendar the objectives, I use a template like the one below and here is a sample math unit plan (without specific dates). The example below is one week of the unit and all the weekly plans together make the unit plan for those weeks. This week-by-week breakdown serves as a checklist of all the objectives that I will try to cover in the unit.
Step 3: Revisiting and Revising
The unit plan is essentially a guide for the four (4) or however many weeks the unit happens to be for you. However, it can change based on the flow of the daily lessons, in addition to students' mastery of the material. At the end of each week (or even mid-way through the week), look back at the unit plan and think about what can be revised. You may find that some expectations are taking longer than expected for students to master (i.e. overestimating students' understanding) and some expectations are taking less time for them to master (i.e. underestimating students' understanding). You may also discover that students require a bit of refreshing of the strand from the previous year. If so, you can spend a small portion of the day, perhaps 10-15 minutes before the lesson, to revise those expectations. For example, if working on representing time in a 12-hour notation, some students may benefit from a revision of This essentially helps with fine tuning the unit plan to meet the needs of our students.
The unit plan is essentially a guide for the four (4) or however many weeks the unit happens to be for you. However, it can change based on the flow of the daily lessons, in addition to students' mastery of the material. At the end of each week (or even mid-way through the week), look back at the unit plan and think about what can be revised. You may find that some expectations are taking longer than expected for students to master (i.e. overestimating students' understanding) and some expectations are taking less time for them to master (i.e. underestimating students' understanding). You may also discover that students require a bit of refreshing of the strand from the previous year. If so, you can spend a small portion of the day, perhaps 10-15 minutes before the lesson, to revise those expectations. For example, if working on representing time in a 12-hour notation, some students may benefit from a revision of This essentially helps with fine tuning the unit plan to meet the needs of our students.
Widget is loading comments...